OPAMP NEDİR ?
Akım ve gerim kazancı sağlayan devreler olup, güç kazancı ya da empedans dönüştürme de yapabilirler . Opamp ile devreler üzerinde temel matematik işlemlerini gerçekleştirecek sistemler kurabiliriz.
OPAMP’ların temel özellikleri yüksek giriş direnci, düşük çıkış direnci ve yüksek gerilim kazancıdır .
OPAMP , girişine uygulanan zayıf elektrik sinyallerini, devresindeki aktif devre elemanları yardımı ile çıkışına büyütülmüş olarak aktarır. Bunu yaparken güç kaynağından aldığı enerjiyi kullanır. Bu enerjiyi, giriş sinyali ile aynı özellikte fakat daha güçlü bir çıkış sinyali elde etmek üzere işler. Sonuçta, yükseltecin çıkışından alınan elektriksel sinyalin gücü, girişine uygulanan sinyalin gücünden daha yüksektir.
OP-AMP ( Operational Amplifier )
196O ‘lı yılların sonlarına doğru kullanılmaya başlanmıştır. 741 ve 747 gibi entegre şeklinde üretilirler. Bu entegrelere dışarıdan bağlanan devre elemanları ile geri beslemesi ve dolayısıyla yükselteç devresinin gerilim kazancı kontrol edilebilir.
Genel olarak OPAMP, çok yüksek kazançlı bir DC yükselteçtir. OPAMP ile hemen hemen yapılamayacak devre yok gibidir.
İşlemsel yükselteçlerin temel görevi iki girişi arasındaki gerilimin yada sinyalin farkını alarak elde ettiği değeri kendi kazancı kadar yükselterek çıkışa vermektir. İşlemsel yükselteçlerin temel özellikleri arasında son derece yüksek gerilim kazancı, yüksek giriş direnci ve düşük çıkış direnci, sayılabilir. İç devre yapısı tek bir yonga üzerine bir ila dört adet işlemsel yükselteç oluşturabilmek için, yüzlerce son derece küçük transistör ve devre elemanından oluşur. Bu devreler sadece BJT (bipolar junction transistor), JFET (jonction field effect transistor) ya da MOSFET (metal oxide semiconductor FET) kullanılarak yapılabilir.
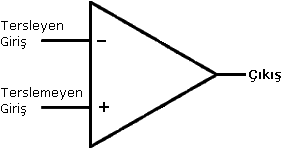Şekil 1
Şekil 1 ‘de temel OPAMP sembolü gösterilmiştir. Bu sembolde gösterilmeyen bir de besleme voltaj uçları bulunur.
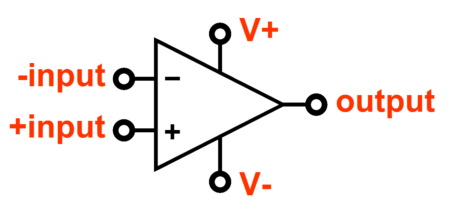Şekil 2 ( a )
Şekil 2 ( b )
Genel olarak bir işlemsel yükseltecin iki giriş, bir çıkış, iki de besleme kaynağı ucu bulunur. Sembolde, (-) işaretli giriş ucu tersleyen (eviren, inverting), (+) işaretli giriş ucu terslemeyen (evirmeyen, noninverting) giriş ucudur. (-) işaretli giriş ucuna sinyal uygulandığında çıkıştan 180° faz farklı bir çıkış sinyali alınır.
Şekil 3
Giriş sinyali (+) işaretli giriş ucuna uygulandığı zaman da çıkıştan alınan sinyalle girişe uygulanan sinyal arasında faz farkı olmaz. Yani aynı fazda bir çıkış sinyali alınır.
OpAmp’ın İdeal Karakteristiği
OPAMP‘ın iki girişi ve bir çıkışı bulunur.
Düşük frekanslarda kazanç genelde büyüktür.
Giriş akımları ise çok düşüktür.
Bir OPAMP’ın giriş empedansı sonsuz, çıkış empedansı ise sıfırdır.
Açık devre diferansiyel kazancı sonsuzdur.
Bant genişliği sonsuzdur.
Şekil 4
741 Opamp Türkçe Bilgiler Uygulama Örneklerini inceleyin
OPAMP KARAKTERİSTİKLERİ
OpAmp bir yükselticidir. Ancak problemlerin analizinde ve OpAmp devrelerinin dizaynlarında AC ve DC karakteristikleri gözönünde bulundurmamız gerekmektedir. Bu bölümde, ofset problemlerine ve OpAmp’ın performansını etkileyen diğer karakteristikler açıklanacaktır.
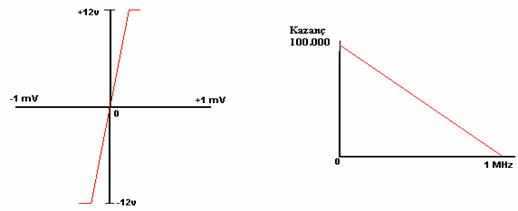Şekil 5
İdeal bir Opamp’ın kazancı sonsuzdur. Gerçek bir Opamp’ın kazancı ise normalde 100.000 (100dB) dir. üstte bulunan grafiğe baktığımız zaman giriş gerilimi milivoltlar civarında salınırken bunun sonucunda elde edilen çıkış gerilimi +Vcc ve -Vcc (+12V ve –12V) arasında değişmektedir.
Çoğu durumda kazanç aşırı derecede fazladır. Bunu engellemek için negatif geri besleme direnci ilave edilir.
Yukarıdaki grafikte Sağ tarafa baktığımızda Opamp’ın kazancı sağa doğru azalmaktadır. Kazanç, frekans arttıkca hızlı bir şekilde düşmektedir. Aslında band genişliği (çıkışın 3dB düştüğü) 1KHz’dir. Band genişliği negatif geri besleme direnci koymak suretiyle arttırılabilir.
Opamp’ların giriş empedansı idealde sonsuzdur. Ancak gerçekte çok yüksektir.
Örneğin 1MW. Çıkış empedansı idealde 0’dır. Ancak gerçekte çok düşüktür. Örneğin 150W.
OPAMP’ların özellikleri
Şekil 6
* Kazancı çok fazladır. (Örneğin, 200.000)
* Giriş empedansı çok yüksektir. (5 MΩ)
* Çıkış empedansı sıfıra yakındır.
* Band genişliği fazladır. (1MHz)
* Girişe 0 Volt uygulandığında, çıkıştan yaklaşık 0 Volt elde edilir.
OPAMP ‘ın iki kazancı vardır. Bunlar açık çevrim ve kapalı çevrim kazancıdır. Kapalı çevrim kazancı, devreye harici olarak bağlanan geri besleme direnci ile belirlenir. Açık çevrim kazancı ise OPAMP ‘ın kendi kazancıdır. Yani direnç ile belirlenemeyen kazancıdır. Her ne kadar OPAMP ‘ın kazancı yaklaşık 200.000 gibi bir değerde olmasına rağmen bu kazanç OPAMP ‘a uygulanan besleme voltajına bağlıdır. Örneğin, bir OPAMP ‘ın besleme voltajı ±12 Volt ve girişe 1 Volt yükseltilmek üzere bir giriş sinyali uygulansa, OPAMP ‘ın özelliğine göre çıkıştan bu kazançla orantılı olarak 200.000 Volt alınmaz. Çünkü, besleme voltajı ±12 Volt kullanılmışsa çıkıştan en fazla 12 Volt alınır. Burada, açık çevrim kazancını etkileyen en önemli faktör besleme voltajının değeridir.
OPAMP ‘ın diğer özelliği 5MΩ ‘a ulaşan giriş empedansıdır. Giriş empedansının bu kadar büyük olması, bağlı olduğu sinyal kaynağını ve bir önceki devreyi yüklememesi, küçük bir giriş akımı ile kumanda edilmesi gibi üstünlükleri vardır.
OPAMP ‘ın çıkış empedansı idealde sıfır iken pratikte bu değer 100-150Ω arasındadır. OPAMP ‘ın çıkış empedansının küçük olması, çıkış akımını arttırarak kısa devrelerden zarar görmemesini sağlar.
OPAMP ‘ın band genişliği 1MHz civarındadır. OPAMP ‘a uygulanan sinyalin frekansı yükseldikçe kazanç düşer. DC ve DC ‘ye yakın sinyallerde OPAMP ‘ın kazancı yaklaşık 200.000 ‘dir.
OPAMP ‘ın statik çalışmasında yani girişte sinyal yokken çıkışın 0 Volt olması gerekir. Ancak, pratikte giriş uçları arasında, çok küçük de olsa bir offset gerilimi oluşur. Bu küçük gerilim OPAMP ‘ın kazancı ile çarpılarak çıkışa aktarılır. Bu nedenle, OPAMP entegrelerinde offset sıfırlama uçları bulunur.
Şekil 7 – OPAMP Offset Geriliminin Sıfırlanması
Yüksek performans gereken yerlerde şekil 7 ‘de görüldüğü gibi harici bağlantılarda OPAMP ‘ın çıkış gerilimi boşta iken sıfır yapılır. 741 entegresinin 1 ve 5 nolu uçlarına bir potansiyometre bağlanarak, orta ucu (-) voltaj kaynağına irtibatlandırılır.
 |  |
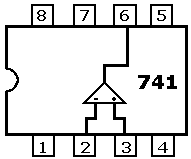| Pin No. 1- Offset sıfırlama 2- OPAMP ‘ın tesleyen giriş ucu 3- OPAMP ‘ın terslemeyen giriş ucu 4- (-) V, negatif besleme voltajı 5- Offset sıfırlama 6- OPAMP çıkışı 7- (+) V, pozitif besleme voltajı 8- Boş uç | Pin No. 1- OPAMP I ‘in tersleyen giriş ucu 2- OPAMP I ‘in terslemeyen giriş ucu 3- OPAMP I ‘in offset sıfırlama ucu 4- (-) V, negatif besleme voltajı (İki OPAMP için ortak) 5- OPAMP II ‘nin offset sıfırlama ucu 6- OPAMP II ‘nin terslemeyen giriş ucu 7- OPAMP II ‘nin tersleyen giriş ucu 8- OPAMP II ‘nin offset sıfırlama ucu 9- OPAMP II ‘nin+V besleme voltaj girişi 10- OPAMP II ‘nin çıkışı 11- Boş uç 12 OPAMP I ‘nin çıkışı 13- OPAMP I ‘nin +V besleme voltajı 14- OPAMP I ‘nin offset sıfırlama ucu |
Şekil. 8 – IC 741 ve IC 747 Entegrelerinin İç Bağlantı Şemaları.
Şekil 8 ‘de görüldüğü gibi 741 entegresinde 1 OPAMP bulunurken, 747 entegresinde 2 adet OPAMP bulunur.
OP-AMP ‘ların Beslenmesi
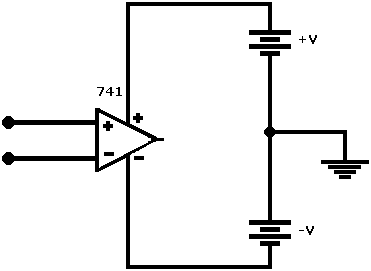
Şekil 9 – OPAMP ‘ın Simetrik Kaynaktan Beslenmesi
OPAMP sembolünde +V ve -V uçları, besleme kaynağının bağlandığı uçlardır. Bir OPAMP ‘a, ±5 V, ±12 V, ±15 V, ±18 V gibi besleme voltajı verilebilir. OPAMP ‘ın AC sinyal yükseltmesinde tek güç kaynağı kullanmak yeterlidir. Genellikle OPAMP ‘lar simetrik kaynaktan beslenir.
Şekil 9 ‘de bir OPAMP ‘ın simetrik kaynaktan beslenmesi görülmektedir, örneğin bir OPAMP devresi olarak 741 entegresi kullanılacaksa, entegrenin 7 nolu ucuna pozitif besleme, 4 nolu ucuna ise negatif besleme uygulanır. Şekil 9 ‘de görülen (+) giriş faz çevirmeyen giriş ucu, (-) giriş faz çeviren giriş ucunu gösterir.
OPAMP’LARIN TEMEL KULLANIMLARI
İşlemsel kuvvetlendiriciler terim olarak analog bilgisayarların alan örneklerindendir. Bu tipteki yükselticiler matematiksel işlemlerin, toplama, çıkartma, çarpma, bölme, integral, türev ve logoritma alma gibi uygulamalarında başarılı bir şekilde kullanılmışıtır. Aslında Opamp‘lar çok geniş bir alanda kullanılmalarına karşın hala orijinal isimleri kullanılmaktadır.
Temelde OPAMP yüksek gerilim kazancı DC fark kuvvetlendiriciler olup aşağıdaki karakteristikleri taşımaktadır.
Sonsuz band genişliği,
Sonsuz giriş empedansı,
Sıfır çıkış empedansı
OPAMP Devreleri
@ Tersleyen Yükselteç (Faz Çeviren, Inverting Amplifier) Olarak
@ Terslemeyen Yükselteç (Faz Çevirmeyen, Noninverting Amplifier) Olarak
@ Gerilim İzleyici (Voltage Follower) Olarak
@ Toplar Yükselteç (Summing Amplifier) Olarak
@ Fark Alıcı Yükselteci (Difference Amplifier) Olarak
@ Karşılaştırıcı (Comparator) Olarak
@ İntegral Alan (Integrator) Devre Olarak
@ Türev Alan (Differentiator) Devre Olarak
@ Doğrultmaç Olarak
@ Yarım Dalga Doğrultmaç Olarak
@ Tam Dalga Doğrultmaç Olarak
@ Logaritmik Yükselteç Olarak
@ Gerilim Regülatörü Olarak
@ Gerilim Kontrollü Osilatör Olarak Kullanılır
@ Opamp’ların Lineer Kullanımları Ses Yükselticiler , Video Yükselticiler , RF ve IF Yükselticiler , Gerilim Regülatörleri
OPAMP ile neler yapabiliriz ?
OPAMP (İşlemsel yükselteç)’ lerin kullanım alanları oldukça geniş bir yelpazeye dağılmakta ve elektroniğin her dalında çeşitli tip ve özellikteki OPAMP’lar kullanılmaktadır.
Başlıklar halinde kullanıldıkları alanları inceleyecek olursak,
Analog Bilgisayar İşlemleri : Toplama, çıkarma, bölme, çarpma, türev alma, integral alma, logaritma alma, üs alma ve trigonometrik fonksiyonlardır.
Yükselteç İşlemleri : Enstrumantasyon (ölçme) yükselteci, ses frekans yükselteci, motor kontrol
yükselteçleri ve basit yükselteç devreleridir.
Dalga Şekillendirici İşlemleri : Kırpıcı, sinüs – kare dalga dönüştürücü, kare – üçgen dalga dönüştürücü ve kenetleyicilerdir.
Regülasyon İşlemleri : Voltaj regülasyon işlemleri (RMS),-DC dönüştürücü, gerilim çoklayıcı işlemleri ve konvertisör işlemleridir.
Veri Transfer İşlemleri : Gerilim frekans dönüştürücü ve kablolu veri transfer devreleridir.
Sinyal Analiz İşlemleri : Özel karşılaştırma işlemleri, pencere karşılaştırıcı, tepe dedektörü ve gerilim dağıtıcı.
Sinyal Üreteç İşlemleri : Wien köprü osilatörü, kare dalga ve üçgen dalga üreteci, testere dişi ve darbe üreteci, merdiven dalga üreteci, gerilim kontrollü frekans üreteç işlemleri, modülasyon işlemleri ve zamanlama devreleri.
Test ve Ölçme İşlemleri : Akım, gerilim, direnç, frekans, faz, kapasite, güç, transistör test, OPAMP test, ısı ve diğer fiziksel büyüklükler ölçme devreleri.
Filtre İşlemleri : Aktif filtre işlemleri, alt geçiren, üst geçiren, band geçiren filtre, işlemleri.
İşlemsel yükselteçlerin kullanım alanları burada listelenen konularla sınırlı olmayıp,
uygulamada pek çok alanda kullanılmaktadır. İşlemsel yükselteçlerin kullanım alanları
sadece tasarımcıların hayal gücü ile sınırlıdır.
Enstrumantasyon Amplifikatörleri
Tanımı, Yapısı ve Çalışma Prensibi
Enstrumantasyon yükselteçler, yüksek performanslı voltaj yükselteçleridir. Aynı zamanda bu yükselteçler, yüksek kazançlı, yüksek giriş empedanslı ve düşük çıkış empedansı gösteren fark yükselteçleridir. Kelime anlamı, yardımcı yükselteçlere karşılık gelmektedir. Enstrumantasyon yükselteçler, negatif geri beslemeden dolayı daha kararlı bir devre karakteristiğine sahiptir. Burada kullanılan geri besleme, negatif geri beslemedir. Çünkü, dirençlerle belirlenen voltaj kazancı (kapalı çevrim kazancı), dirençsiz açık çevrim kazancından daha düşüktür. Geri beslemeli kazanç daima açık çevrim kazancından (geri beslemesiz kazanç) daha kararlıdır.
Her OPAMP ‘ta olduğu gibi geri beslemeli kazanç, geri beslemesiz kazançtan daha düşük olduğu için kullanılan geri besleme negatiftir. Çünkü, Pozitif geri beslemede kazanç artar, negatif geri beslemede ise kazanç azalır.
Enstrumantasyon amplifikatörler aynı zamanda, basınç transducerinden (dönüştürücü), sıcaklık sensorundan gelen sinyalleri yükseltmede kullanılır. Bu yükselteçler, girişlerine uygulanan sinyallerinin farkını almak suretiyle çalışır.
OPAMP ‘ların Uygulama Alanları
- Yüksek Giriş Empedanslı Versiyonu
- Yüksek Giriş Voltajlı Versiyonu
- Yüksek Ortak Mod Tepki Oranlı Versiyonu
Yüksek Giriş Empedanslı Versiyonu
Yüksek giriş empedanslı enstrumantasyon yükselteç, iki adet OPAMP ‘tan oluşur. Vi1 ve Vi2 olmak üzere iki giriş kaynağı bulunur.
Buradaki Vi1 ve Vi2 kaynakları, OPAMP ‘ların giriş empedansından daha büyük dirence sahip olduğundan bu devrenin çok yüksek bir giriş empedansı vardır. Bu devrenin çıkış voltaj değerini bulmak için süperpozisyon teoremi kullanılır. İki giriş kaynağı olduğu için, bir kaynağın devreye tatbik edildiği diğerinin yok sayıldığı, diğer durumda da tersi düşünülebilir.
Şekil 10
Şekil 10- Yüksek Giriş Empedanslı Enstrumantasyon Yükselteç
Vi2 Kısa devre olarak düşünülürse;
Vout1 = [1+(R2 / R1)].[-(R4 / R3)].Vi1 olur.
Direnç değerleri formülde yerine konulursa;
Vout1 = [1+(1 / 100)].[-(100 / 1)].Vi1
Vout1 = (101 / 100).[-(100 / 1)].Vi1
Vout1 = -101.Vi1 olarak bulunur.
Bu kez Vi1 kısa devre gibi düşünülürse;
Vout2 = [1+(R4 / R3)].Vi2 olur.
Direnç değerleri formülde yerine konulursa;
Vout2 = [1+(100 / 1)].Vi2
Vout2 = 101.Vi2 olarak bulunur.
Bulunan iki formül birleştirilirse;
Vo = Vout1+Vout2
Vo = -101.Vi1+101.Vi2
Vo = 101(Vi2 – Vi1) bulunur.
Yüksek Giriş Voltajlı Versiyonu
Şekil 11
Şekil 11 ‘daki versiyonda, inverting modda çalışan 2 adet OPAMP kullanılmıştır. Bu devre çıkışında, Vi1 ve Vi2 giriş voltajlarından küçük bir fark sağlar. Yani, iki büyük giriş voltajı arasında küçük bir fark sağlar. Çıkış voltaj değerini bulmak için ve burada Vi1 ve Vi2 olmak üzere iki adet giriş kaynağı olduğu için süperpozisyon yöntemi kullanılır.
Vi2 = 0 durumunda;
Vout1 = [-(R3 / R1)].[-(R6 / R4)].Vi1 olur.
Direnç değerleri formülde yerine konulursa;
Vout1 = [-(5K / 50K)].[-(50K / 5K)].Vi1
Vout1 = Vi1 olur.
Vi1 = 0 durumda ise;
Vout2 = [-(R6 / R5)].Vi2 olur.
Direnç değerleri formülde yerine konulursa;
Vout2 = [-(50K / 50K)].Vi2
Vout2 = -Vi2 olur.
Süperpozisyon teoremine göre bulunan Vout1 ve Vout2 değerleri birleştirilirse, devrenin çıkış voltajı;
Vo = Vout1+Vout2
Vo = Vi1+(-Vi2)
Vo = Vi1-Vi2 olarak bulunur.
Yüksek Ortak Mod Tepki Oranlı Versiyonu
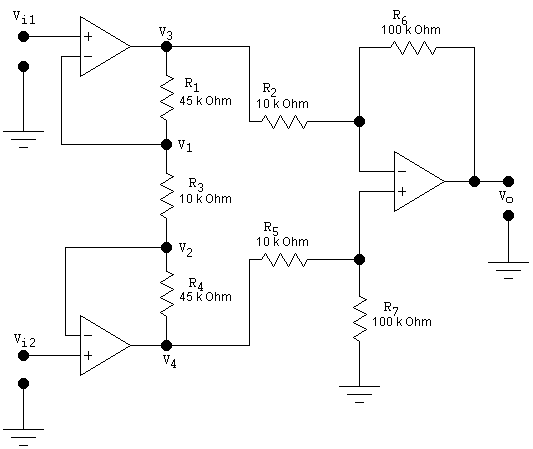Şekil 12
Şekil 12 ‘de enstrumantasyon yükselteçlerden en fazla kullanılanı gösterilmiştir. OPAMP ‘larda ortak mod tepki oranı (common-mode rejection ratio -CMRR), her iki girişinde de ortak olan giriş sinyalini reddetme özelliğidir. Faz çeviren (-) ve çevirmeyen (+) girişe aynı anda uygulanan işaretin, çıkış işaretine oranına eşittir. CMRR’nin birimi dB’dir. Bu versiyondaki enstrumantasyon yükselteçlerde, parazit ve gürültüleri atma oranı da büyüktür.
Şekil 12 ‘deki enstrumantasyon yükselteçte Vi1 ve Vi2 girişleri OPAMP ‘ların faz çevirmeyen (+) girişlerine uygulanmıştır. R3 direnciyle devrenin kazancı kontrol edilebilir.
İlk iki OPAMP çıkışından alman sinyal fark yükseltecine uygulanmıştır.
Devrenin, çıkış voltajını bulabilmek için yine süperpozisyon teoremi kullanılır. diyot.net
Vi2 = 0 durumunda; devre non-inverting çalışma modundadır.
Şekil 12(a)
Şekil 12(a) – Vi2 = 0 durumunda
V3a = Vi1 [1+(R1 / R3)]
OPAMP ‘ın giriş empedansı sonsuz olduğundan,
V1a = Vi1 olur.
V2a çıkış hayali toprak olduğundan V2a = 0 ‘dır.
V4a = [-(R4 / R3)].Vi1 olur.
Şekil 12(b)
Şekil 12(b) – Vi1 = 0 durumda
V3b = [-(R1 / R3)].Vi2
V1b = 0 (Hayali toprak olduğundan)
V2b = Vi2
V4b = [1+(R4 / R3)].Vi2 olur.
3. OPAMP ‘ın faz çeviren (-) ucuna 10 KΩ ‘luk direnç üzerinden uygulanan voltaj;
V3 = V3a + V3b
V3 = Vi1.[1+(R1 / R3)]+Vi2.[-(R1 / R3)]
Direnç değerleri yerine konulursa;
V3 = Vi1.[1+(45K / 10K)]+Vi2.[-(45K / 10K)]
V3 = 5,5.Vi1-4,5.Vi2 olarak bulunur.
3. OPAMP ‘ın (fark amp) faz çevirmeyen (+) ucuna R5 direnci üzerinde uygulanan voltaj;
V4 = V4a + V4b
V4 = [-(R4 / R3)].Vi1+[1+(R4 / R3)].Vi2
Direnç değerleri formulde yerine konulursa;
V4 = [-(45K / 10K)].Vi1+[1+(45K / 10K)].Vi2
V4 = -4,5.Vi1+5,5.Vi2
V4 = 5,5.Vi2-4,5.Vi1 olarak bulunur.
Enstrumantasyon yükselteç yapısında bulunan son OPAMP bir fark yükseltecidir. Bu fark yükselteç modundaki OPAMP ‘ın faz çeviren (-) giriş ucuna V3 sinyali, faz çevirmeyen (+) giriş ucuna ise V4 sinyali gelmektedir. Fark yükseltecinin, devredeki direnç etiketlerine göre formülü,
Vo = [-(R6 / R2)].V3+[1+(R6 / R2)].[R7 / (R5 + R7)].V4 olur.
Direnç değerleri formülde yerine konulursa;
Vo = [-(100 / 10)].(5,5.Vi1 – 4,5.Vi2)+[1+(100 / 10)].[100 / (100 + 10)].(5,5.Vi2 – 4,5.Vi1)
Vo = -10.(5,5.Vi1 – 4,5.Vi2)+10.(5,5.Vi2 – 4,5.Vi1)
Vo = -55.Vi1+45.Vi2+55.Vi2-45.Vi1
Vo = 100.Vi2 – 100.Vi1
Vo = 100.( Vi2 – Vi1 ) olarak bulunur.
İŞLEMSEL YÜKSELTEÇLER DERS NOTLARI pdf
OPAMPLAR pdf
OPAMPLAR pdf
OPAMP DEVRELERİ pdf
